This class implements the analytic solution of a system of linear ODEs with constant matrix. More...

#include <linear_ode_analytic.hh>

Inheritance diagram for LinearODEAnalytic:

Collaboration diagram for LinearODEAnalytic:

Public Types
typedef LinearODESolverBase	FactoryBaseType

Public Member Functions
	LinearODEAnalytic ()
	Default constructor is possible because the input record is not needed. More...

	LinearODEAnalytic (Input::Record in_rec)
	Constructor from the input data. More...

	~LinearODEAnalytic (void)
	Destructor. More...

void	update_solution (arma::vec &init_vector, arma::vec &output_vec) override
	Updates solution of the ODEs system. More...

bool	evaluate_time_constraint (double &time_constraint) override
	Estimate upper bound for time step. Return true if constraint was set. More...

Public Member Functions inherited from LinearODESolver< LinearODEAnalytic >
	LinearODESolver ()

virtual	~LinearODESolver ()

virtual void	update_solution (arma::mat &init_vecs, arma::mat &output_vecs, const std::vector< unsigned int > &mask=std::vector< unsigned int >(0)) override
	Updates solution of the system with different initial vectors. More...

Public Member Functions inherited from LinearODESolverBase
	LinearODESolverBase ()

virtual	~LinearODESolverBase ()

void	set_system_matrix (const arma::mat &matrix)
	Sets the matrix of ODE system. More...

void	set_step (double step)
	Sets the step of the numerical method. More...

Static Public Member Functions
static const Input::Type::Record &	get_input_type ()

Static Public Member Functions inherited from LinearODESolverBase
static Input::Type::Abstract &	get_input_type ()

Protected Member Functions
void	compute_matrix ()

Protected Attributes
arma::mat	solution_matrix_
	The solution is computed only by a matrix multiplication (standard fundamental matrix). More...

Protected Attributes inherited from LinearODESolverBase
arma::mat	system_matrix_
	the square matrix of ODE system More...

arma::vec	rhs_
	the column vector of RHS values (not used currently) More...

double	step_
	the step of the numerical method More...

bool	step_changed_
	flag is true if the step has been changed More...

bool	system_matrix_changed_
	Indicates that the system_matrix_ was recently updated. More...

Static Private Attributes
static const int	registrar
	Registrar of class to factory. More...

Detailed Description

This class implements the analytic solution of a system of linear ODEs with constant matrix.

The analytic solution can be obtained in the special case due to a physical nature of the problem. The problem is then solved only by a matrix multiplication.

The assumption is made that the equations are independent. Each quantity is decreased (supposing negative diagonal) to 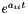$e^{a_{ii} t}$ . The decrement 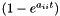$\left( 1-e^{a_{ii} t} \right)$ is then distributed among other quantities according to the given fraction.

In case of the decays and first order reactions the elements of the solution matrix are:

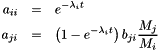
$\begin{eqnarray*} a_{ii} &=& e^{-\lambda_i t} \\ a_{ji} &=& \left( 1-e^{-\lambda_i t} \right) b_{ji} \frac{M_j}{M_i} \end{eqnarray*}$

where 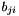$b_{ji}$ is the branching ratio of 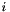$ i $ -th reactant and 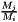$\frac{M_j}{M_i}$ is the fraction of molar masses.

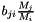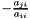The fractions $b_{ji} \frac{M_j}{M_i}$ are then obtained from the system matrix by dividing $-\frac{a_{ji}}{a_{ii}}$ .

Drawback: These assumptions (equation independence) are adequate when very small time step is applied. This will lead to huge amount of evaluations of the exponential functions which can be expensive, so other numerical methods might be more appropriate. When the time step is large then the assumption is quite inadequate.

Definition at line 49 of file linear_ode_analytic.hh.

Member Typedef Documentation

typedef LinearODESolverBase LinearODEAnalytic::FactoryBaseType

Definition at line 52 of file linear_ode_analytic.hh.

Constructor & Destructor Documentation

LinearODEAnalytic::LinearODEAnalytic ( )

inline

Default constructor is possible because the input record is not needed.

Definition at line 60 of file linear_ode_analytic.hh.

LinearODEAnalytic::LinearODEAnalytic ( Input::Record in_rec )

Constructor from the input data.

Definition at line 38 of file linear_ode_analytic.cc.

LinearODEAnalytic::~LinearODEAnalytic ( void )

Destructor.

Definition at line 42 of file linear_ode_analytic.cc.

Here is the caller graph for this function:

Member Function Documentation

void LinearODEAnalytic::compute_matrix ( )

protected

Computes the standard fundamental matrix.

Definition at line 57 of file linear_ode_analytic.cc.

Here is the caller graph for this function:

bool LinearODEAnalytic::evaluate_time_constraint ( double & time_constraint )

overridevirtual

Estimate upper bound for time step. Return true if constraint was set.

Implements LinearODESolverBase.

Definition at line 80 of file linear_ode_analytic.cc.

Here is the caller graph for this function:

const Record & LinearODEAnalytic::get_input_type ( )

static

Input record for class LinearODE_analytic.

Definition at line 28 of file linear_ode_analytic.cc.

void LinearODEAnalytic::update_solution	(	arma::vec &	init_vec,
		arma::vec &	output_vec
	)

overridevirtual

Updates solution of the ODEs system.

Parameters

init_vec	is the column initial vector
output_vec	is the column output vector containing the result

Implements LinearODESolverBase.

Definition at line 46 of file linear_ode_analytic.cc.

Here is the caller graph for this function:

Member Data Documentation

const int LinearODEAnalytic::registrar

staticprivate

Initial value:

=
        Input::register_class< LinearODEAnalytic, Input::Record >("LinearODEAnalytic") +
        LinearODEAnalytic::get_input_type().size()

Registrar of class to factory.

Definition at line 83 of file linear_ode_analytic.hh.

arma::mat LinearODEAnalytic::solution_matrix_

protected

The solution is computed only by a matrix multiplication (standard fundamental matrix).

Definition at line 79 of file linear_ode_analytic.hh.

The documentation for this class was generated from the following files:

/home/cygwin64/F123-windows-release/flow123d/src/reaction/linear_ode_analytic.hh
/home/cygwin64/F123-windows-release/flow123d/src/reaction/linear_ode_analytic.cc

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Protected Attributes

Static Private Attributes

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation