The main class for interpolation of functors. More...
#include <interpolant.hh>

Classes | |
| class | FuncError_lp |
| class | FuncError_wp1 |
Public Member Functions | |
| Interpolant () | |
| Default constructor. More... | |
| template<template< class > class Func, class Type > | |
| Interpolant (Func< Type > *func, bool interpolate_derivative=false) | |
| Constructor with functor setting. More... | |
| virtual | ~Interpolant (void) |
| Destructor. More... | |
Evaluation. | |
| double | val (double x) |
| Returns interpolated value. More... | |
| double | val_test (double x) |
| Do NOT use, only for testing purpose. More... | |
| double | val_p1 (double x) |
| Do NOT use, unless you are 100% sure. More... | |
| DiffValue | diff (double x) |
| Returns interpolated value of the derivation. More... | |
| double | f_val (double x) |
| Returns value of the original functor. More... | |
| DiffValue | f_diff (double x) |
| Returns 1st derivative of original functor using FADBAD. More... | |
| double | f_diffn (double x, unsigned int n) |
Interpolation. | |
| virtual int | interpolate () |
| Creates piecewise interpolation with polynomials of selected degree. More... | |
| template<template< class > class Func, class Type > | |
| void | set_functor (Func< Type > *func, bool interpolate_derivative=false) |
| Sets the functor. More... | |
 Public Member Functions inherited from InterpolantBase Public Member Functions inherited from InterpolantBase | |
| InterpolantBase () | |
| Default constructor. More... | |
| virtual | ~InterpolantBase () |
| Destructor. More... | |
| double | error () |
| Returns error of the interpolation. More... | |
| double | bound_a () const |
| Returns left boundary of the interval. More... | |
| double | bound_b () const |
| Returns right boundary of the interval. More... | |
| unsigned int | size () const |
| Returns the size of the interpolation table. More... | |
| void | set_interval (double bound_a, double bound_b) |
| Sets the interpolation interval boundaries. More... | |
| void | set_size (unsigned int size) |
| Sets size of the interpolation table. It is also equal to the number of intervals. More... | |
| void | set_norm (ErrorNorm::Type norm_type=ErrorNorm::max, double p=2) |
| Sets the type of norm used for computing estimate of the error of the interpolation. More... | |
| void | set_size_automatic (double user_tol, unsigned int init_size, unsigned int max_size=default_max_size) |
| Sets automatic choice of the size of the table. More... | |
| void | set_extrapolation (Extrapolation::Type extrapolation) |
| Sets the type of extrapolation. Functor type is default. More... | |
| EvalStatistics | statistics () const |
| Returns structure with evaluation statistics. More... | |
| void | reset_stat () |
| Resets all measured statistics. More... | |
| void | check_stats_and_reinterpolate (double percentage=0.3) |
| Can be called to check automatically the evaluation statistics and possibly reinterpolate. More... | |
Protected Member Functions | |
| void | compute_error (double tol, std::vector< double > &f, std::vector< double > &df) |
| Creates piecewise linear interpolation. More... | |
| void | compute_error (double tol, double p, ErrorNorm::Type norm_type) |
| Computes estimate of interpolation error with given norm. More... | |
| void | swap_middle_values (std::vector< double > &f, std::vector< double > &df) |
| void | compute_values () |
| Creates table of nodes and function values. More... | |
| DiffValue | diff_p1 (double x) |
Finds interval on which x lies. More... | |
 Protected Member Functions inherited from InterpolantBase Protected Member Functions inherited from InterpolantBase | |
| long | fact (long x) |
| Recursive factorial function (used in Taylor row expansion in n-th derivative computation). More... | |
| void | check_all () |
| Checks that the parameters are set before interpolation. More... | |
Protected Attributes | |
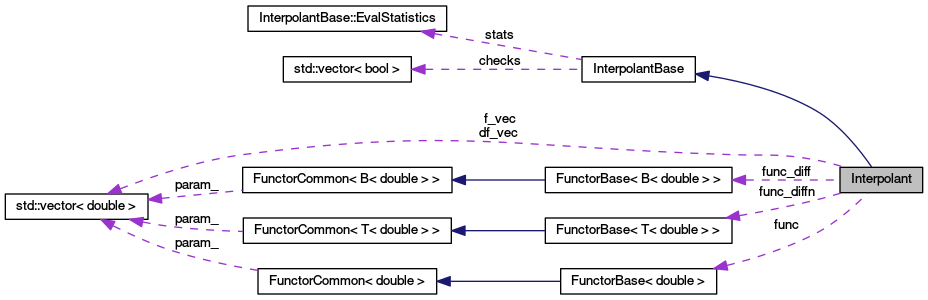
| FunctorBase< double > * | func |
| Pointer to original functor with double type. More... | |
| FunctorBase< B< double > > * | func_diff |
| Pointer to original functor with FADBAD B type. More... | |
| FunctorBase< T< double > > * | func_diffn |
| Pointer to original functor with FADBAD T type. More... | |
| bool | interpolate_derivative |
| Is true if we want to interpolate the derivative too. More... | |
| std::vector< double > | f_vec |
| Vector of function values at nodes. More... | |
| std::vector< double > | df_vec |
| Vector of function derivatives values at nodes. More... | |
 Protected Attributes inherited from InterpolantBase Protected Attributes inherited from InterpolantBase | |
| double | bound_a_ |
| Left interval boundary. More... | |
| double | bound_b_ |
| Right interval boundary. More... | |
| double | step |
| Chosen interpolation step. More... | |
| double | a_div_step |
| bound_ divided by step - precomputed value for evaluation More... | |
| unsigned int | size_ |
| Number of dividing intervals. More... | |
| unsigned int | n_nodes |
Number of nodes in the interval  . More... . More... | |
| double | user_tol |
| User set tolerance which is used during automatic step choice. More... | |
| unsigned int | max_size |
| Maximal size of the interpolation table. More... | |
| bool | automatic_size |
| Is true if step/size should be chosen automatically. More... | |
| ErrorNorm::Type | norm_type |
| Type of norm used to compute error of the interpolation. More... | |
| double | p |
Exponent used in norms  and and  when computing error. More... when computing error. More... | |
| double | error_ |
| Error of the interpolation. More... | |
| Extrapolation::Type | extrapolation |
| EvalStatistics | stats |
| Structure which keeps evaluation statistics. See InterpolantBase::eval_statistics. More... | |
| std::vector< bool > | checks |
| Vector of boolean values telling us which parameters are set or not. More... | |
Additional Inherited Members | |
 Static Protected Attributes inherited from InterpolantBase Static Protected Attributes inherited from InterpolantBase | |
| static const unsigned int | n_derivatives = 10 |
| Defines how many derivatives we allow to be returned from Taylor's coeficients. More... | |
| static const unsigned int | default_max_size = 10*1000 |
| Default maximal size of the interpolation table. More... | |
| static const double | simpson_tolerance = 1e-10 |
| Tolerance in Adaptive Simpson intergration. More... | |
Detailed Description
The main class for interpolation of functors.
This class is a wrapper of a functor (defined by class FunctorBase) which provides computation of derivates and interpolation of the functor. We will describe the functionality in the following paragrahphs.
Evaluation of a functor and its derivatives
Beside the interpolation, the class provides calling of the functor itself. All functions evaluating directly the functor starts with 'f_', e.g. function f_val computes the functor value.
We use the FADBAD++ library (website) to compute derivatives of the functor. First derivatives can be obtained by function f_diff which uses backward automatic differentiation. Higher order derivatives can be obtained via f_diffn which uses Taylor expansion method.
Interpolation
Sofar we provide only a piecewise linear interpolation. Both the function and its derivative can be interpolated. User has to provide the functor object to the constructor or later to the function set_functor. Then one must set at least the interval ![$ [a,b]$](form_28.png) by set_interval and the size of the interpolation table by set_size before calling interpolate. Otherwise assert will crash the program in debug build.
by set_interval and the size of the interpolation table by set_size before calling interpolate. Otherwise assert will crash the program in debug build.
When user wants the size to be chosen automatically then set_size_automatic must be called at first. An initial guess of size of the interpolation table and a tolerance which is assumed to be the maximum relative difference between the function and the interpolant (sum of value and derivative difference) must be provided. Futher user can set the maximum size of the interpolation (default 1000) table which will not be exceeded and the type of norm in which the estimate of the error of interpolation will be computed (enumerated in ErrorNorm, default maximal norm). See one of the following paragraphs to learn how we deal with the error of the interpolation.
Outside the given interval the interpolation is extrapolated. User can choose among several types of extrapolation which are enumerated in Extrapolation. Constant and linear extrapolation use the first and last interpolating polynomials to compute the value. Functor type means that the functor itself will be evaluated outside the interval. Type of extrapolation can be changed by set_extrapolation function. Calling functor is the default type of extrapolation.
Error of the interpolation
We are interested in the maximum difference between the function value and its interpolation. When interpolating also the derivative, we need to compute the difference between derivative and its interpolation too. Therefore we would like to compute something like the L-infinity norm, relative to function value and its derivative. Let  be the function and its derivative and
be the function and its derivative and  interpolation of the function and interpolation of the derivative on the interval
interpolation of the function and interpolation of the derivative on the interval  . We suggest an approximation of the infinity norm:
. We suggest an approximation of the infinity norm:
![\[ \|f-g\|_\infty = \sup_{x\in I} F(x) = \sup_{x\in I} \left( \frac{|f(x)-g(x)|}{|f(x)| + tol} + \frac{|f'(x)-g'(x)|}{|f'(x)| + tol} \right) \approx \max_{x\in J} \left( \frac{|f(x)-g(x)|}{|f(x)| + tol} + \frac{|f'(x)-g'(x)|}{|f'(x)| + tol} \right) \]](form_32.png)
where  is set of points that lies in the middle of two neighboring nodes.
is set of points that lies in the middle of two neighboring nodes.  is a given tolerance for zero (avoids zero division). When computing the size of the interpolation table automatically, we compare the user tolerance
is a given tolerance for zero (avoids zero division). When computing the size of the interpolation table automatically, we compare the user tolerance  given by set_size_automatic funtion directly with the estimated value of the supremum norm.
given by set_size_automatic funtion directly with the estimated value of the supremum norm.
This approach is fast and when computing the size automatically, we use the computed values (middle points, function and derivative values) in next interpolation. On the other hand this does not work good around zero points of the function where the value is small and the fraction becomes large or does not converge when dividing the intervals (  is a good example).
is a good example).
Therefore we provide also error estimation with  and
and  norm. Then the user given tolerance is compared as it is stated in the following inequation:
norm. Then the user given tolerance is compared as it is stated in the following inequation:
![\[ \left( \frac{\int \limits_I F^p(x) \,\rm{d} x}{|I|} \right)^{\frac{1}{p}} \leq TOL. \]](form_39.png)
This approach is much more expensive but can give better results.
TODO: Improve error computation. Suggest more robust method.
Evaluation statistics
We collect some statistics during the evaluation of the interpolant in the struct InterpolantBase::EvalStatistics – total number of calls, number of evaluations inside the interpolation interval and number of evaluation outside the interval. One can use these statistics to decide whether it is necessary to widen the interval and recompute the interpolation. Function check_stats_and_reinterpolate is provided to do this automatically according to the given percentage of evaluation outside the interval.
Definition at line 291 of file interpolant.hh.
Constructor & Destructor Documentation
| Interpolant::Interpolant | ( | ) |
Default constructor.
Definition at line 155 of file interpolant.cc.
| Interpolant::Interpolant | ( | Func< Type > * | func, |
| bool | interpolate_derivative = false |
||
| ) |
Constructor with functor setting.
- Parameters
-
func is the pointer to functor interpolate_derivative is true when derivate is also interpolated
- Template Parameters
-
Func is the functor type Type is the template type of the functor (e.g. double)
Definition at line 56 of file interpolant_impl.hh.
|
virtual |
Destructor.
Definition at line 164 of file interpolant.cc.
Member Function Documentation
|
protected |
Creates piecewise linear interpolation.
Computes estimate of interpolation error in maximum norm.
Definition at line 410 of file interpolant.cc.

|
protected |
Computes estimate of interpolation error with given norm.
Definition at line 490 of file interpolant.cc.
|
protected |
Creates table of nodes and function values.
Creates vector of nodes according to the table size and computes function and derivative values at the nodes.
Definition at line 335 of file interpolant.cc.

|
inline |
Returns interpolated value of the derivation.
- Parameters
-
x is the point at which we evaluate the interpolation
Definition at line 157 of file interpolant_impl.hh.

|
inlineprotected |
Finds interval on which x lies.
Function that evaluates the derivative of P1 interpolant at x.
Definition at line 281 of file interpolant_impl.hh.
|
inline |
Returns 1st derivative of original functor using FADBAD.
- Parameters
-
x is the point at which we evaluate the original functor
Definition at line 213 of file interpolant_impl.hh.
| double Interpolant::f_diffn | ( | double | x, |
| unsigned int | n | ||
| ) |
Returns n-th derivative of original functor using FADBAD. Uses coeficients in Taylor's row.
- Parameters
-
x is the point at which we evaluate the original functor n is the order of the derivative we want
Definition at line 171 of file interpolant.cc.
|
inline |
Returns value of the original functor.
- Parameters
-
x is the point at which we evaluate the original functor
Definition at line 208 of file interpolant_impl.hh.
|
virtual |
Creates piecewise interpolation with polynomials of selected degree.
Implements InterpolantBase.
Definition at line 189 of file interpolant.cc.
| void Interpolant::set_functor | ( | Func< Type > * | func, |
| bool | interpolate_derivative = false |
||
| ) |
Sets the functor.
Can be used when the functor is not set in the constructor.
- Parameters
-
func is the pointer to functor interpolate_derivative is true when derivate is also interpolated
- Template Parameters
-
Func is the functor type Type is the template type of the functor (e.g. double)
Definition at line 71 of file interpolant_impl.hh.
|
protected |
|
inline |
Returns interpolated value.
- Parameters
-
x is the point at which we evaluate the interpolation
Definition at line 84 of file interpolant_impl.hh.

|
inline |
Do NOT use, unless you are 100% sure.
This function evaluates the P1 interpolant at x. It does not check the interval, does not provide extrapolation and does not collect statistics.
Can be used to POSSIBLY speed the evaluation just a little bit, if you are absolutely sure that you evaluate the interpolant only on the given interval and do not want to collect statistics.
Same can be done with diff_p1 if it is made public.
Used in unit_test benchmark to compare with val function.
Definition at line 250 of file interpolant_impl.hh.

|
inline |
Do NOT use, only for testing purpose.
TODO: After testing it can be removed and val_p1 can be made private again.
Definition at line 137 of file interpolant_impl.hh.
Member Data Documentation
|
protected |
Vector of function derivatives values at nodes.
Definition at line 390 of file interpolant.hh.
|
protected |
Vector of function values at nodes.
Definition at line 389 of file interpolant.hh.
|
protected |
Pointer to original functor with double type.
Definition at line 380 of file interpolant.hh.
|
protected |
Pointer to original functor with FADBAD B type.
Definition at line 383 of file interpolant.hh.
|
protected |
Pointer to original functor with FADBAD T type.
Definition at line 384 of file interpolant.hh.
|
protected |
Is true if we want to interpolate the derivative too.
Definition at line 386 of file interpolant.hh.
The documentation for this class was generated from the following files:
- /opt/flow123d/flow123d/src/tools/interpolant.hh
- /opt/flow123d/flow123d/src/tools/interpolant.cc
- /opt/flow123d/flow123d/src/tools/interpolant_impl.hh

 1.8.11
1.8.11