#include <intersection.hh>
Public Member Functions | |
| Intersection (const ElementFullIter ele_master, const ElementFullIter ele_slave, const IntersectionLocal *isec) | |
| unsigned int | master_dim () |
| dimension of the master element More... | |
| unsigned int | slave_dim () |
| dimension of the slave element More... | |
| const Element * | master_iter () const |
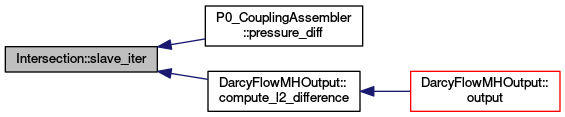
| const Element * | slave_iter () const |
| arma::vec | map_to_master (const arma::vec &point) const |
| arma::vec | map_to_slave (const arma::vec &point) const |
| double | intersection_true_size () const |
Private Member Functions | |
| void | intersection_point_to_vectors (const IntersectionPoint *point, arma::vec &vec1, arma::vec &vec2) |
Private Attributes | |
| unsigned int | dim |
| dimenze pruniku More... | |
| ElementFullIter | master |
| ElementFullIter | slave |
| arma::Mat< double > | master_map |
| matrix part of linear transform from reference element of intersection to reference element of master or slave More... | |
| arma::Mat< double > | slave_map |
| arma::vec | master_shift |
| shift vector of the linear transform More... | |
| arma::vec | slave_shift |
Detailed Description
Navrh algoritmu pro hledani pruniku elementu dvou siti (libovlnych dimenzi) algoritmus postupuje od bodu pruniku pres usecky a polygony k mnohostenum
Vstup: Sit1 dimenze d1 a Sit2 dimenze d2 predpoladam d1<=d2
1) hladam body na hranici pruniku tj. Intersection<d> <d_e1,d_e2> .. prunik ma dimenzi d a pronikaji se simplexy dimenze d_e1, a d_e2
Intersection<0><0,0> .. totozne vrcholy El<0> Intersection<0><0,1> a <1,0> .. vrchol jedne site lezi na hrane druhe site Intersection<0><0,n> a <n,0> .. vrchol lezi na El<n> druhe site
Intersection<0><1,1> .. bodovy prusecik dvou usecek v rovine Intersection<0><1,2> a <2,1> ... prusecik hrany a trojuhelnika ... dalsi zvlastni pripady vcetne <0><3,3> .. tetrahedrony s vrcholem na povrchu druheho
2) liniove pruniky Intersection<1>: Intersection<1><1,1> .. usecky na spolecne primce Intersection<1><1,2> a <2,1>.. usecka v rovine trojuhelnika Intersection<1><1,3> a <3,1> .. usecka a tetrahedron Intersection<1><2,2> .. prusecik dvou trojuhelniku Intersection<1><2,3> a <3,2> .. trojuhelnik a hrana tetrahedronu ..
... doprcic je to fakt hodne moznosti a je otazka, zda je nutne je vsechny rozlisovat
Algoritmus by mel probuhat takto:
1) Najdu vrchol V site 1 a element E site 2 aby V byl v E (to neni tak trivialni, pokud site nepokryvaji stejnou oblast ale snad by to slo hledat v pruniku obalovych boxu) 2) najdu pruseciky P_i hran z vrcholu V s povrchem E, konstruuju vsechny potrebne pruniky elementu majici vrchol V s elementem E
Sousedni elementy spolu s hranami ktere do nich vedou ulozim do prioritni fronty.
3) Vyberu z prioritni fronty novy E, pricemz vyuzivam spositane pruseciky psislusne steny a okoli vrcholu V tj. jdu po hranach po kterych jsem do noveho lementu prisel a najdu vsechny hranove pruniky, pak konstuuju slozitejsi pruniky az mam vsechny pruniky s novym elementem ...
...
Prioritni fronta by preferovala elementy do kterych jsem se nejvicekrat dostal, tim se snazim minimalizovat povrch projite oblasti. Je ale mozne, ze to algoritmus naopak zpomali, pokud je prioritni fronta log(n).
Zpracovani jednoho elementu tedy zahrnuje 1) trasovani hran: pro hranu H: testuju hledam prusecik se ctyrstenem: ANO -> pamatuju si hranovy prunik a ke stene (resp. sousednimu elementu) kde hrana vychazi pridam vychozi hranu NE -> konci ve vrcholu, dalsi hrany vychazejici z vrcholu pridam na seznam hran vchazejicich do elementu
2) po nalezeni pruniku vsech hran, hledam pruniky vsech vchazejicich ploch: jedna plocha ma se vstupni stenou useckovy prunik na jehoz konci jsou: *vstupni hrana
- okraj steny kazdopadne trasuju okraj plosneho pruniku pres povrch elementu, nebo po vstupnich hranach, pokud prunikova plocha obsahuje vrchol tvorim nove vstupni plochy ...
3) Podobne trasuju vchazejici objemy
?? lze nejak vyuzit pokud ma element vice vstupnich sten minimalne se da kontrolovat ...
Struktura systemu pruniku do budoucna: 1) trida IntersectionManager, ma matici vektoru. Na poli A(i,j) je vektor lokalnich souradnic na elementu dimenze i (chodi od 1 do 3) pruniku dimenze j (chodi od 0 do 3 resp do 2 pokud nebudu chtit prekryvy siti stejne dimenze)
2) Jeden intersection objekt je pak iterator dvou elementu a dva indexy lokalnich souradnic v prislusnych vektorech.
Prozatim to zjednodusime tak, ze vektory lokalnich souradnic budu alokovat zvlast a nebudu je zdruzovat
Nakonec potrebuju pocitat integral pres prunik z nejake funkce f(phi_a(x), phi_b(x)), kde phi_a je bazova funkce na jednom elementu a phi_b na druhem. To budu delat numerickou kvadraturou, takze potrebuji zobrazit prunik na jednotkovy simplex. Pro uzel kvardatury x_i musim najit body a_i a b_i na referencnich elementech A a B. Tj potrebuju lokalni souradnice (to jsou souradnice na referencnich elementech) kvadraturnich bodu. V nic pak umim spocitat hodnotu bazovych funkci a pak i hodnotu funkce f.
K tomu staci mit matici transformace pruniku na referencni element. Takze bych pro jednotlive dvojice element - prunik mel matici + posouvaci vektor z armadila.
Definition at line 146 of file intersection.hh.
Constructor & Destructor Documentation
| Intersection::Intersection | ( | const ElementFullIter | ele_master, |
| const ElementFullIter | ele_slave, | ||
| const IntersectionLocal * | isec | ||
| ) |
otestuje se jestli dimenze masteru je mensi nez dimenze slave - chybova hlaska (vyjimka - throw) pocet pointu=dim+1
Definition at line 27 of file intersection.cc.
Member Function Documentation
|
private |
| double Intersection::intersection_true_size | ( | ) | const |
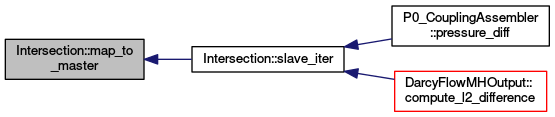
| arma::vec Intersection::map_to_master | ( | const arma::vec & | point | ) | const |
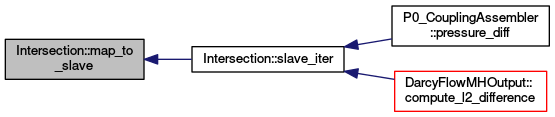
| arma::vec Intersection::map_to_slave | ( | const arma::vec & | point | ) | const |
| unsigned int Intersection::master_dim | ( | ) |
dimension of the master element
Definition at line 57 of file intersection.cc.
|
inline |
Definition at line 157 of file intersection.hh.
| unsigned int Intersection::slave_dim | ( | ) |
dimension of the slave element
Definition at line 62 of file intersection.cc.
|
inline |
Member Data Documentation
|
private |
dimenze pruniku
Definition at line 167 of file intersection.hh.
|
private |
Definition at line 168 of file intersection.hh.
|
private |
matrix part of linear transform from reference element of intersection to reference element of master or slave
Definition at line 171 of file intersection.hh.
|
private |
shift vector of the linear transform
Definition at line 173 of file intersection.hh.
|
private |
Definition at line 168 of file intersection.hh.
|
private |
Definition at line 171 of file intersection.hh.
|
private |
Definition at line 173 of file intersection.hh.
The documentation for this class was generated from the following files:
- /opt/flow123d/flow123d/src/mesh/intersection.hh
- /opt/flow123d/flow123d/src/mesh/intersection.cc


 1.8.11
1.8.11